AntsRL – Multi-Agent Reinforcement Learning

En observant une colonie de fourmis, on peut remarquer à quel point elles semblent organisées. Pour réunir suffisamment de nourriture et se défendre des dangers, une fourmilière typique de 250'000 individus doit coopérer et s'auto-organiser. Par l'utilisation de rôles spécifiques et d'un puissant outil - les phéromones - des milliers de fourmis plutôt limitées peuvent coopérer et atteindre de grands buts.

Nous nous intéressions à l'émergence de tels comportements en environnement simulé. En donnant à des "fourmis" les outils nécessaires et un environnement à explorer, pourrions-nous voir apparaître ce type de phénomène à partir de rien ?

À la croisée des chemins entre les systèmes Multi-Agents et l'Apprentissage par Renforcement, nous avons conçu un système permettant à une fourmilière d'individus très simples développer des stratégies intelligentes pour optimiser son approvisionnement en nourriture.

Note importante : tout au long de ce post, nous utiliserons parfois des mots pouvant suggérer que les agents ont une vie mentale interne, des intentions, du libre-arbitre, etc. Cela a pour seul but de rendre les explications plus faciles à lire et ne reflète absolument pas la réalité des choses. Pas plus que quelques milliers de nombres gouvèrnent le comportement de nos agents, ce qui interdit tout interprétation téléologique. Voyons, il s'agit simplement de multiplications de matrices.

Définition du problème

Premièrement, posons les principales hypothèses qui fixent le cadre de nos expérimentations. Il est essentiel de savoir d'où nous partons pour pouvoir apprécier la beauté d'un éventuel comportement émergent : on ne voudrait pas se retrouver abasourdis par quelque chose qui n'est pas si surprenant, non ?

Hypothèses

La première et plus importante de nos hypothèses est l'isolation totale des agents. Il s'agit d'une des principales hypothèses du paradygme multi-agents : les agents n'ont aucun moyen direct de communication qui ne passe pas par l'environnement lui-même. Par conséquent, tout moyen de communication est sujet à l'imprévu, et donc faillible. En d'autres mots, nous avons pris un soin particulier à ne pas laisser nos agents communiquer comme dans un esprit de ruche, en transmettant directement des informations entre eux. La seule façon dont ils pourront communiquer consiste à déposer des phéromones derrière eux, et à regarder devant eux pour voir d'autres agents et des traces de phéromones précédemment déposés.

La seconde hypothèse est la relativité des perceptions. Il est important que nos agents n'aient aucun indice sur leur localisation et leur orientation dans le monde. D'une façon générale, ils ne voient le monde que depuis leur perspective individuelle.

L'Environnement

Comme pour tout projet d'Apprentissage par Renfocement (RL par la suite), la définition de l'environnement est centrale.

1. Les murs : roches générées procéduralement qui empêchent les fourmis de traverser.
2. Les fourmis : la représentation de nos agents sont ces petites fourmis noires.
3. La fourmilière : le cercle bleu au centre est la fourmilière depuis laquelle toutes les fourmis viennent et où elles doivent ramener la nourriture.
4. La nourriture : ces cercles verts, également générés procéduralement, sont les sources de nourriture. Les fourmis peuvent les ramasser, ce qui retire un pixel, et les déposer dans la fourmilière.
5. Les phéromones : nous avons donné deux types de phéromones à nos fourmis. Un rouge et un bleu. Ils sont tous deux déposés par les fourmis sous leurs pattes, et s'évaporent lentement.
6. La marque d'exploration : complètement invisible à nos fourmis, cette visualisation jaune représente la région de la carte déjà explorée par toute la colonie.

Le code pour générer un environnement est rendu aussi simple que possible pour que chacun puisse expérimenter avec différentes configurations de cartes. En utilisant différents générateurs procéduraux, on peut générer des roches de densité variable, plus ou moins de sources de nourriture, éloignées de la fourmilière ou non, etc. Enfin, une seed peut être spécifié pour s'assurer que l'environnement généré est contrôlé si nécessaire, ce qui s'avère utile pour évaluer différents agents sur une même carte.

generator = EnvironmentGenerator(w=200,  
                                 h=200,  
                                 n_ants=n_ants,  
                                 n_pheromones=2,  
                                 n_rocks=0,  
                                 food_generator=CirclesGenerator(n_circles=20,
                                                                 min_radius=5,
                                                                 max_radius=10),
                                 walls_generator=PerlinGenerator(scale=22.0,
                                                                density=0.1),  
                                 max_steps=steps,  
                                 seed=181654)

Enfin, l'environnement est un espace 2D continu, bien que les murs, la nourriture, la fourmilière et les phéromones existent sur une grille 2D discrète. Les fourmis se déplacent avec des coordonnées et des rotations décimales, ce qui permet des mouvements plus précis. La carte se répète également dans les deux directions, reliant la frontière haute à la frontière basse, et la frontière gauche à la frontière droite (surface d'un tore). Les fourmis ne voient rien de tout cela : quand elles regardent à travers le bord de la carte, elles voient simplement l'autre côté de celle-ci. Quand elle se déplace au-delà de la frontière, elles sont téléportées de l'autre côté.

D'un point de vue technique, la visualisation est totalement séparée de la simulation. Nous pouvons simuler l'environnement contenant les fourmis sans rien visualiser, ce qui est largement plus rapide, et en profiter pour enregistrer un fichier de replay. Après coup, nous pouvons visualiser n'importe lequel de ces fichiers, jouer sur la vitesse de lecture, et choisir quoi regarder. Les fichiers de replay sont cependant très lourds.

Les Agents

Vous avez déjà pu les voir dans l'image ci-dessus, mais donnons à présent un peu plus de détails sur nos agents : les fourmis. Comme expliqué dans nos hypothèses, les agents sont complètement indépendants les uns des autres et ne partagent aucune information directement. Leur définition interne varie en fonction des différents modèles que nous avons implémentés, mais leurs perceptions du monde et leurs moyens d'action restent les mêmes.

Vous pouvez également voir si une fourmi a ramassé de la nourriture : elle aura un petit rond vert entre ses mandibules. N'est-ce pas mignon ?

Perception

Elles voient devant elles dans un certain rayon. Voici une image représentant les dimensions de leur perception, en termes de cases discrètes dans la grille 2D. Premièrement, on calcule les coordonnées décimales de chaque case perçue, en appliquant les translations et les rotations relatives à leur position actuelle, puis nous arrondissons ces coordonnées pour obtenir les cases de la grille du monde qu'elles perçoivent. Cela donne parfois des résultats surprenants, mais nous considérons que nos fourmis sont comme les vrais : très mauvaises à voir les choses ! Elles devraient cependant être capable de détecter facilement les phéromones devant elles, les murs, la nourriture et les autres fourmis.

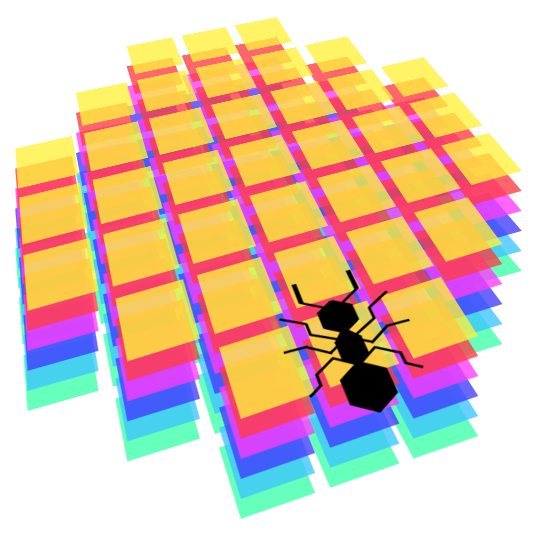
En termes mathématiques, leur perception est toujours une matrice carrée de 7x7, avec un masque pour la rendre plus arrondie, et autant de couches que nécessaire pour représenter tous les "canaux" de leur vision. Dans notre cas, chaque type d'objet dans le monde (fourmilière, autres fourmis, nourriture, murs, phéromones, etc.) sont représentés sur un canal différent. Cela produit des données de perception très régulières qui rendent possible l'entraînement d'un réseau de neurone sur celles-ci.

Actions

Les fourmis ont quatre types d'actions pour agir sur le monde :

1. Avancer ou reculer
2. Tourner sur elles-mêmes
3. Attraper ou relâcher avec leur mandibules (ramasser de la nourriture ou la déposer)
4. Déposer des phéromones du type choisi

Par simplicité, nous avons décidé d'automatiser les actions 1 et 3 : les fourmis avancent toujours d'une case devant elles par étape de simulation. Elles ramassent automatiquement la nourriture si leurs mandibules sont vides et qu'il y en a sur le sol, puis la déposent si elles se trouvent dans la fourmilière. Nous aurions pu les laisser apprendre ces actions aussi, mais nous avons pensé qu'il n'y avait rien de réellement compliqué à ces simples règles et elles nous feraient gagner un certain temps d'entraînement.

Au final, nos fourmis doivent gérer leur direction pour se rendre au bon endroit et doivent décider quel phéromone déposer pour communiquer avec les autres fourmis sur le long terme. Tout ceci est, comme nous allons le voir, déjà assez difficile.

Multi-Agent

Mais nos fourmis ne sont pas seules. Ici, nous avons défini l'une d'entre elles, mais il y en a entre 10 et 100 dans les simulations que nous avons réalisées. Bien sûr, chacune d'entre elles fonctionne de la même manière, bien que nous ayons introduit des différences individuelles à un certain point. Cette structure commune permet de traiter toutes les fourmis en même temps dans un batch. Ce n'est pas seulement un batch du type utilisé dans les réseaux de neurones, mais c'est aussi utile au niveau de la simulation où chaque fourmi n'est pas une instance d'une classe, mais plutôt une ligne dans de grands tableaux.

Au moment de réaliser une action, on applique les actions individuelles de chaque fourmi sur le grand tableau. Par exemple, pour déplacer chaque fourmi vers l'avant dans sa direction propre, on ajoute \cos(\theta)\cdotx+\sin(\theta)\cdot y aux tableau original des coordonnées x, y. Chaque opération est appliquée à toutes les fourmis, ce qui n'empêche pas les actions individuelles mais évite de nombreuses boucles inutiles.

Les opérations d'indexation matricielles deviennent vite complexes en ce qui concerne les champs de perception individuels parallélisés sur chaque fourmi. Mais ça fonctionne.

Comment motiver les fourmis

À cette étape, nous avons des fourmis fonctionnelles, mais ce sont des coquilles vides. Le moment est venu de leur donner vie et de leur faire réaliser des actions. Nous démarrerons avec des fourmis particulièrement stupides en implémentant notre premier model : RandomAgent.

Magnifiquement aléatoire, ce comportement ne fait pas grand chose mais on peut déjà voir de quoi les fourmis sont capables. On peut voir les fourmis érrer et déposer des phéromones bleus et rouges partout. Aussi, comme elles ramassent automatiquement la nourriture sur laquelle elles marchent et la déposent dans la fourmilière si elles la traversent encore, le score en bas à droite augmente (notez qu'un petit bug le fait démarrer à un certain nombre, mais nous ne considérerons pas cela). Cela fixe la performance de base pour nos prochaines expériences : comme vous pourrez le voir, nous allons d'abord perdre de nombreux points, mais ensuite nos fourmis parviendront à faire bien mieux que le hasard.

Si vous avez entendu parler d'apprentissage par renforcement auparavant, vous savez que l'un des éléments clés pour apprendre une stratégie optimale est d'avoir une fonction de récompense bien conçue. C'est de cette façon que nous apprendrons à nos agents à réaliser certains types de comportement. Ici, nos fourmis n'ont qu'un seul objectif : sans arrêt alimenter la fourmilière avec de la nourriture. Cette simple tâche demande de la planification à long-terme et de la coopération sociale. Par conséquent, nous l'avons divisée en un ensemble de sous-objectifs : de plus petites récompenses que nous utiliserons pour dire à nos fourmis "oui, tu as bien fait, continue comme ça !".

Une récompense pour explorer

Comme les sources de nourritures peuvent apparaître loin de la fourmilière (nous avons même un générateur de terrain qui interdit à ces cercles d'apparaître trop proche de la fourmilière), les fourmis doivent explorer l'environnement. Cependant, comme elles n'ont pas de GPS intégré, elles n'ont aucune idée de l'endroit où elles se trouvent. Elles doivent trouver un moyen de continuer d'avancer sans se retrouver bloquées contre un mur et en évitant les zones où une fourmi s'est déjà rendue.

On note cette récompense r_{explore} et on la calcule à chaque pas de simulation. Pour chaque cellule de la grille qu'une fourmi découvre, on lui attribut un point. Mais comme les fourmis n'ont aucune façon de savoir si une cellule a déjà été visitée par une autre avant elles, elles doivent faire usage de leurs phéromones pour marquer leur chemin.

Une récompense pour ramasser la nourriture

C'est une récompense très simple qui accorde un point à chaque fourmi qui marche dans de la nourriture et la ramasse. Comme le ramassage est automatique dans nos paramètres, cela pousse juste les fourmis à être attirées par la nourriture lorsqu'elles en voient. Mais plus généralement, cela leur donne une motivation à trouver cette juteuse salade aussi rapidement qu'elles le peuvent ! On note cette récompense r_{food}.

Une récompense pour retourner à la maison

Exactement comme après une soirée un peu trop arosée et sans batterie sur le téléphone, nos fourmis ont beaucoup de mal à trouver le chemin de retour vers chez elles. Elles ont besoin d'un peu d'aide, mais on ne la leur donne pas directement : nous avons conçu une récompense qui accorde un bon point à chaque fois qu'une fourmi réduit la distance entre leur position et la fourmilière, une fois en possession de nourriture. Comme toujours, les fourmis ne peuvent pas percevoir les récompenses : elles doivent trouver des façons de gagner des points de façon plus efficace en utilisant les outils à leur disposition.

Avec cette motivation à rentrer à la fourmilière après avoir ramassé de la nourriture, on commence à voir apparaître des comportements utilisant les phéromones pour tracer le chemin du retour ! On note cette récompense r_{anthill-heading}.

Une récompense pour déposer la nourriture

La récompense finale, la plus importante de toutes. Après ce long périple à travers champs, il est temps de jeter la nourriture dans la Montagne du Destin la fourmilière. Chaque fois qu'une fourmi atteint la fourmilière en transportant de la nourriture, celle-ci est relâcher et la fourmi gagne un point. On note cette récompense r_{anthill}. Notez que durant l'évaluation, on ne mesure la performance du modèle que vis-à-vis de cette récompense comme nous n'avons pas grand intérêt à ce que les fourmis explorent la carte ou ramassent de la nourriture si ce n'est pas pour la déposer dans la fourmilière.

Une récompense pour les gouverner toutes

Si vous avez tout suivi jusqu'ici, vous devinez que ces sous-objectifs ne doivent pas avoir la même importance. Par exemple, explorer devrait être un simple prérequis au fait de ramener la nourriture à la fourmilière. Si une fourmi doit choisir entre ramasser de la nourriture et explorer la carte un peu plus, elle devrait a priori choisir la nourriture. Comment spécifier cela durant l'entrainement ?

Une façon simple de procéder est de donner des poids plus ou moins importants à chaque récompense en fonction de la tâche accomplie. On écrit donc notre récompense finale :

R = \omega_1 \cdot r_{food} + \omega_2 \cdot r_{explore} + \omega_3 \cdot r_{heading-anthill} + \omega_4 \cdot r_{anthill}

où \omega_1, \omega_2, \omega_3 et \omega_4 sont des facteurs arbitraires qui sont décidés au début de l'entraînement. Ce sont des hyper-paramètres qu'il a fallu ajuster avec beaucoup d'attention comme ils changent complètement la façon dont nos fourmis apprennent et se comportent.

Apprendre aux fourmis avec un DDQN

DDQ... quoi ?

Le but de cet article n'est pas d'expliquer en détails ce qu'est un algorithme de Q-learning profond (“DQN”; Mnih et al. 2015. Si vous n'êtes pas familier de cette notion, nous vous invitons à lire ce très bon article qui explique tout ce qu'il y a à savoir à propos du réinforcement learning pour débuter !

Cependant, si nous devions le résumer brièvement, disons que nous avons un modèle dont l'objectif est d'estimer ce qu'on appelle la Q-value de chacun des états du monde s pour chaque action possible a. La Q-value représente à quel point un état ou une action est intéressante, en termes de récompense future. On appelle fonction de Q-value la fonction qui utilise les paramètres appris \theta pour estimer les Q-values. On la note Q(s, a, \theta).

Dans notre cas, la fonction de Q-value sera un réseau de neurones qui prend en entrée les observation du monde faites par la fourmi, et retourne en sortie une valeur pour chaque action possible. Le DQN améliore et stabilise l'entraînement de notre fonction de Q-value via deux mécanismes innovants : la mémoire de reprise et une cible périodiquement mise à jour.

La mémoire de reprise (ou replay memory) est exactement ce que son nom suggère : une grande table contenant le cours des actions précédemment prises par les fourmis dans des états particuliers, avec les récompenses associées. Après chaque étape d'entraînement, on sauvegarde e_t = (S_t,A_t,R_t,S_{t+1}) dans cette table, avec S les états, A les actions et R les récompenses. Quand on met à jour le réseau de neurones, on peut en tirer des batchs aléatoires et les utiliser en donnée d'entraînement. La reprise d'expériences passées améliore l'efficacité de la donnée, retire des biais de corrélation dans les séquences observées et lisse les changement abrupts dans la distribution de la donnée.

La seconde amélioration utilise deux réseaux de neurones séparés. On entraine le réseau principal à chaque étape, mais on en réalise une copie qu'on appelle le réseau cible (ou target network) qui décide de l'action à réaliser à chaque étape de la simulation. Ce réseau cible est uniquement mis à jour avec une nouvelle copie du réseau principal de temps en temps. Cela rend l'entraînement plus stable et évite les oscillations de court-terme.

Q-learning à actions multiples

Bien, nous avons une façon d'estimer la Q-value pour différentes valeurs d'une action, étant donné un état. Cependant, dans notre cas, nous n'avons pas une mais plusieurs actions à réaliser à chaque étape. Les fourmis peuvent choisir leur direction de déplacement mais aussi quels phéromones utiliser, si elles le jugent nécessaire.

Nous avons donc besoin que notre réseau de neurones retourne une Q-value pour chaque action. Comment faire cela ? La publication Branching Q-learning A. Tavakoli, 2019, propose un module de décision partagé suivi de plusieurs branches dans le réseau, une pour chaque dimension d'action. Au final, on obtient deux têtes de réseau séparées qui prédisent les Q-values pour des actions indépendantes. Pour décider des actions à réaliser, il nous faut simplement choisir la plus grande valeur de chaque branche, ce qui nous donne une combinaison d'actions !

Apprendre une tâche simple : l'exploration

Comme nous n'étions pas certains d'aller dans la bonne direction (enfin, ça devrait marcher théoriquement, mais c'est facile à dire), nous avons décidé de jeter un premier coup d'oeil à notre problème : apprendre aux fourmis à explorer la carte.

Nous avons choisi \omega_1 = 1 et \omega_2 = \omega_3 = \omega_4 = 0, lancé un entraînement sur 50 épisodes avec 20 fourmis. Et voici les résultats !

Ce replay a été capturé sur une carte aléatoire en mode d'évaluation. À partir de ce replay, on peut remarquer deux choses majeures :

1. Les agents ont appris à aller là où il n'y a pas de phéromone car il est plus probable qu'il s'agisse d'une portion inexplorée de la carte.
2. Les agents ont appris à utiliser les deux phéromones d'une façon intéressante. Ils utilisent le rouge durant l'exploration, et le bleu lorsqu'ils passent sur un territoire déjà exploré. Qu'est-ce que cela signifie ? Nous ne savons pas. Peut-être qu'ils savent.

Bien, notre modèle fonctione ! Cependant, essayons d'être un peu plus rigoureux scientifiquement et de vous prouver que nos fourmis s'améliorent en afficant le graphique de la récompense moyenne et de la fonction de perte moyenne en fonction de l'épisode d'entraînement :

Une perte qui augmente ? Et bien, ce n'est pas forcément mauvais en apprentissage par renforcement. Dans notre cas, elle augmente principalement car les récompenses que nos agents récupèrent sont de plus en plus grandes, ce qui augmente aussi l'intervalle des erreurs que le réseau commet lorsqu'il tente de prédire les Q-values. Ce qui nous intéresse vraiment est la courbe bleue où l'on peut clairement voir que l'exploration augmente par rapport à la base aléatoire (qui est déjà plutôt bonne en ce qui concèrne l'exploration).

Des agents avec une mémoire

Nous avons réussi à entraîner un agent d'exploration. À présent, prenons une profonde inspiration et plongeons directement dans la tâche réelle : faire ramasser de la nourriture à nos fourmis et la ramener à la fourmilière. On démarre par l'entraînement en utilisant notre fonction de récompense complète R = \omega_1 \cdot r_{food} + \omega_2 \cdot r_{explore} + \omega_3 \cdot r_{anthill-heading} + \omega_4 \cdot r_{anthill} avec les paramètres suivants:

\omega_1 = 1 \omega_2 = 5 \omega_3 = 1 \omega_4 = 100

Nous avons obtenu des résultats mitigés. Les fourmis tendent à rester bloquées dans des zones de nourriture sans jamais les quitter. Nous avons pensé que cela pouvait être parce que les fourmis n'ont aucune information concernant leurs états et actions passés, et peuvent avoir du mal à suivre une stratégie de long terme.

Nous avons donc décidé de modifier l'architecture de notre réseau et nous sommes inspirés des réseaux LSTM. Nous avons ajouté une branche afin de créer une sorte de mémoire qui serait passée d'un état au suivant à chaque fourmi individuelle. En plus de cela, nous avons ajouté une porte d'oubli, qui est un assemblage de couches neuronales suivies d'une activation sigmoïde, de sorte que le réseau puisse apprendre quand se souvenir et que retenir. L'architecture complète du réseau est donnée par le diagramme ci-dessous :

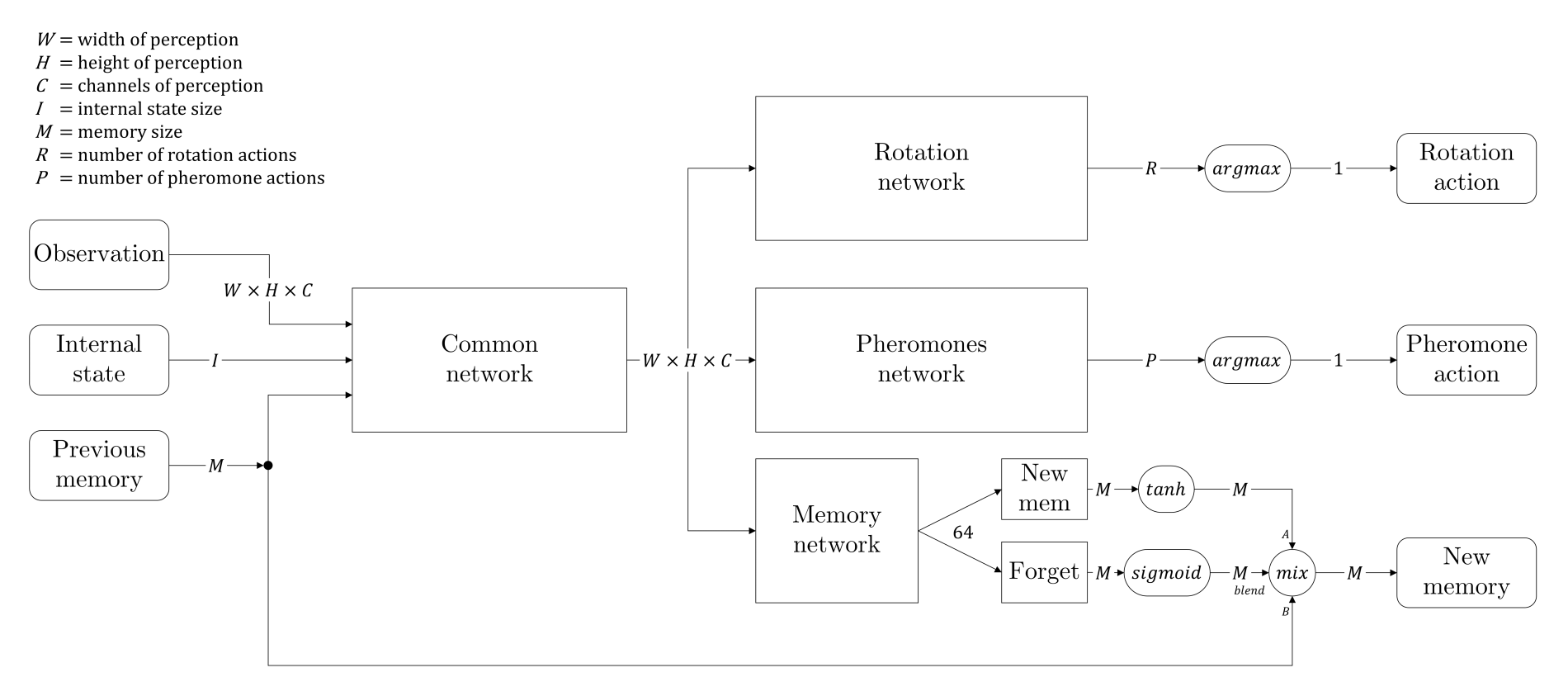
Nous appelons "état interne" les deux informations qui ne sont pas directement visibles dans la matrice de perception : combien de nourriture la fourmis est actuellement en train de tenir, et un seed aléatoire qui donne à chaque fourmi l'opportunité de se différencier (le seed reste le même pendant tout l'épisode pour un même individu).

Enfin, la mémoire est stockée dans la mémoire de reprise comme n'importe quelle observation, ce qui donne à chaque fourmi la possibilité d'être entraînée à se souvenir des informations pertinentes.

Entraînement !

Maintenant que nous avons un réseau plus robuste et une meilleure fonction de récompense, il nous faut juste faire chauffer la machine et démarrer l'entraînement ! Mais attendez... il y a encore d'importants hyper-paramètres à choisir.

Le nombre de fourmis
La bonne nouvelle avec ce type de système multi-agent, c'est qu'on peut le faire fonctionner avec n'importe quel nombre de fourmis. Cependant, comme entraîner une armée de 250'000 fourmis comme dans une fourmilière réelle ne semble pas raisonnable pour la planète -- et nos pauvres ordinateurs --, nous avons décidé d'entraîner avec seulement 20 individus. Notez que jusqu'à un certain nombre de fourmis, le coût de l'augmentation de ce nombre est très faible ! C'est l'avantage principal de toutes les formatter dans un grand tableau.

Le nombre d'épisodes
Ce paramètre est choisi de façon empirique. Puisque l'environnement est codé en Python, le moteur est plutôt lent. Nous avons donc dû limiter le nombre d'épisodes à 150-200 pour avoir un temps d'entraînement raisonnable. C'est relativement peu si on compare à d'autres applications d'apprentissage par renforcement. Cependant, nos résultats montrent que c'était suffisant pour obtenir des comportements intéressants dans ce cas précis.

Epsilon décroissant
L'exploration est un élément clé de l'apprentissage par renforcement. Nous avons utilisé un facteur \epsilon décroissant en utilisant cette formule :

\epsilon = max(\epsilon_{min}, min(\epsilon_{max}, 1 - log(\frac{episode + 1}{15})))

où \epsilon_{min} = [0.01, 0.1] et \epsilon_{max}=1.
Celà permet à nos agents d'explorer beaucoup lors des premiers épisodes, puis de progressivement choisir la meilleure action à chaque fois.

Résultats

Finalement, c'est l'heure de révéler les résultats ! Nos fourmis ont-elles appris quelque-chose ? Peut-on donner une interprétation à ce qui a été appris ? Nous convrirons ce type de questions à partir d'ici.

Résultats finaux sur un long épisode

Bien que nous ayons entraîner nos colonies sur des épisodes de moins de 2'000 étapes, nous avons réalisé une vidéo d'évaluation sur 20'000 étapes pour voir ce qu'il se produirait. Et vous souvenez-vous que nous avons entraîné notre modèle avec 20 fourmis ? À présent, nous pouvons en réalité utilisé notre modèle sur autant de fourmis que nous le voulons ! Donc, puisque c'est plus amusant, nous avons lancé cette simulation avec 50 individus. On peut finalement voir nos fourmis récupérer toute la nourriture de la carte, construisant sans relâche un réseau de phéromones au travers de l'environnement, changeant de cible dès que l'une d'entre elles est épuisée... Nous avons inclus quelques parties où seuls les phéromones sont visibles car nous les trouvons agréables à regarder.

Ce que nous observons est la construction d'une sorte de réseau de phéromones qu'elles utilisent pour s'orienter au travers de la carte. Puisqu'elles ont appris à être attirées par un certain type de phéromones, elles tendent à privilégier certains chemins plus que d'autres. Cela produit une hiérarchie de chemins, avec de véritables autoroutes et plusieurs autres ressemblant à des petites routes de campagne.

Donc, sont-elles comme de vraies fourmis ?

Non, elles ne le sont pas.

Mais... on peut voir des comportements très intéressants ici. En réalité, la partie la plus intéressante ne peut pas être vue dans la vidéo car elle a lieu pendant l'entraînement. Parmi les multiples choses que l'agent apprends, certaines sont directement correlées à l'environnement et d'autres sont des sortes de conventions sociales, ou dit autrement, des stratégies de groupe. Par exemple, l'utilisation de phéromones est une convention que chaque fourmi suit (puisqu'elles ont toutes le même cerveau dans notre projet), mais qui n'a pas de sens particulier dans l'environnement.

Pendant l'entraînement, on peut voir différentes conventions émerger puis disparaître pour en laisser une nouvelle prendre place. Ce que vous voyez dans la dernière vidéo et juste l'une des multiples façons que nos fourmis ont d'utiliser les phéromones pour partager de l'information. Comme ces conventions ne sont enracinées dans l'environnement d'aucune façon, elles peuvent évoluer et disparaître aisément. Ce qui rend ces conventions stables dans le temps est simplement leur tendance à apporter de meilleures récompenses aux fourmis individuelles.

Mais ce n'est pas aussi simple. Notre hypothèse pour expliquer ce que nous avons vu (et mieux l'exploiter dans le futur) est que deux facteurs principaux influencent l'apparition et la disparition de telles conventions.

Premièrement, le terme d'exploration \epsilon, comme il autorise chaque fourmi à agir de façon aléatoire un certain pourcentage du temps, s'il est implémenté naïvement (échantilloner à chaque pas pour toutes les fourmis), tends à faire disparaître ces conventions comme \epsilon percent of the time, toutes les fourmis refusent de les suivre.

Deuxièmement, nos pensons que ces conventions prennent un certain temps à émerger car elles ne profitent pas directement aux individues qui déposent les phéromones. L'agent commun doit apprendre qu'en réalisant certaines actions, d'autres instances de lui-même augmenteront leur récompense. Du point de vue du réseau de neurones, cela requiert principalement que la mémoire de reprise parvienne à un point où la récompense actuelle dépend de ces actions passées. C'est le principe du facteur de décôte \gamma (ou discount factor). Il s'avère qu'il s'agit du même problème que pour la planification de long terme en apprentissage par renforcement, que l'apprentissage par Q-value ne résoud pas complètement.

Considérant ces points, nous pensons que deux choses pertinentes à faire pour obtenir des conventions sociales plus intelligences seraient de réduire \epsilon à un certain moment, ce que nous faisons déjà, et d'autoriser des formes simples de communication supplémentaires entre les agents. Ici, les phéromones sont systématiquement déposés derrière la fourmi, ce qui implique par conception qu'il s'agit d'une action de long terme. Peut-être qu'une forme plus directe de communication -- antenne à antenne -- autoriserait de meilleurs conventions sociales.

Entreprise inachevée : réseau à récompense multiple

Comme mentionné précédemment, nous avons séparé notre réseau en branches qui prédisent chacune les récompenses pour deux ensembles séparés d'actions. Cependant, nous avons demandé à ces branches de prédire une unique récompense par action, sans considération pour la décomposition de cette récompense en multiples facteurs (exploration, ramassage de nourriture, navigation vers la fourmilière et finalement dépôt de nourriture dans cette dernière). Comme nous donnons des poids arbritraires à ces récompenses individuelles, il arrive que l'une d'entre elles occulte complètement les autres lorsqu'elle est découverte pour les premières fois par l'agent. Prédire avec précision les différents ordres de grandeur de la récompense composite en même temps est une tâche quasiment impossible pour notre réseau actuel.

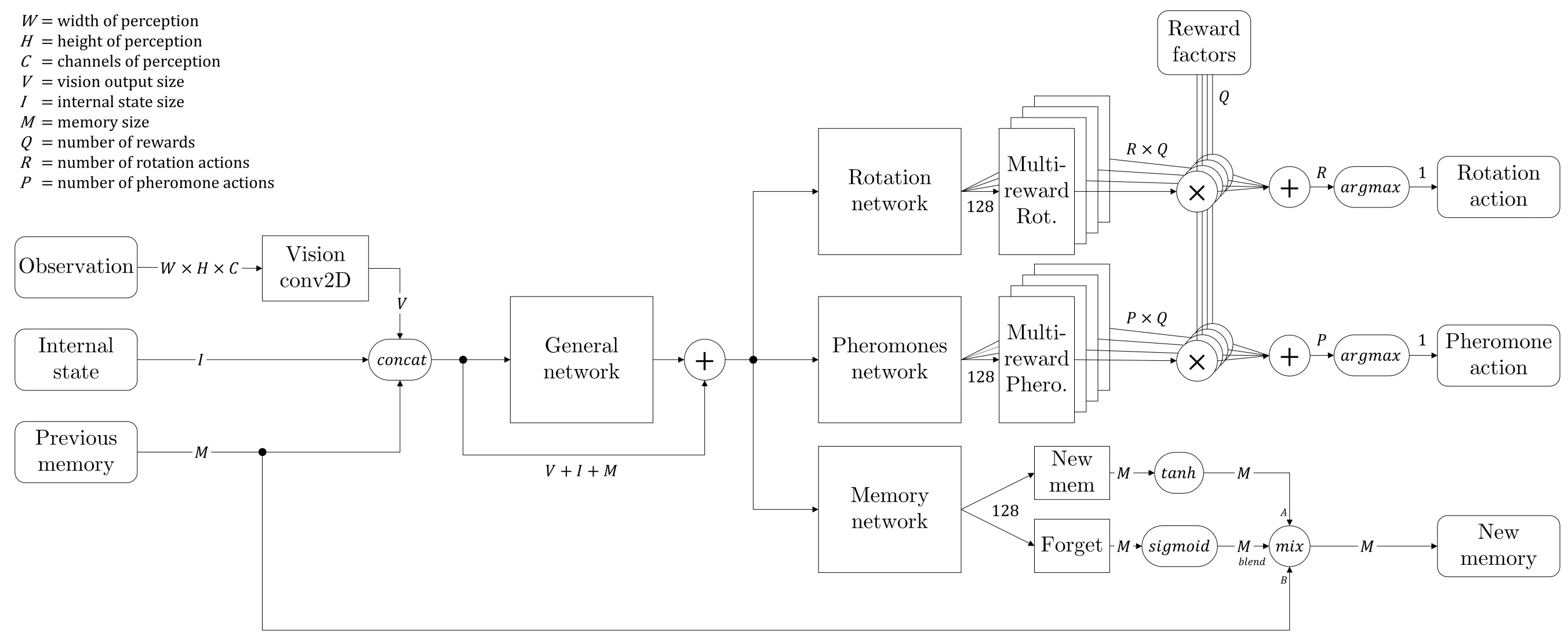
Nous avons essayé de rendre le réseau plus complexe, comme détaillé dans l'image ci-dessus, en le laissant prédire chaque facteur de la récompense indépendamment pour chaque action, puis en les multipliant par les poids supposés connus : chaque partie du réseau doit prédire un type indépendant de récompense et c'est seulement en réalisant la somme pondérée de ces Q-values individuelles que nous obtenons l'action d'intérêt maximal pour l'agent. Dans chaque instance de la mémoire de reprise on retient non-seulement la récompense globale mais aussi chaque facteur indépendamment, ce qui permet l'entraînement de chaque partie spécifique du réseau et de sa cible correspondante.

Les deux principaux avantages de cette méthode sont :

1. Le réseau doit prédire des valeurs dans un interval contrôlé et normalisé, et non une seule valeur qui peut varier de plusieurs ordres de magnitude mais qui nécessite toujours la précision des plus petits d'entre eux. Ici, chaque partie peut se spécialiser pour une récompense spécifique, donnant potentiellement des résultats contradictoires qui sont résolus par la suite lors de la somme pondérée des Q-values.
2. Une fois l'agent entraîné, nous pouvons varier les poids dynamiquement, obtenant ainsi différents comportements de fourmis très facilement. Bien que cela soit plutôt artificiel comme nous le décidons arbitrairement, cela permet des expériences intéressantes où chaque fourmi aurait une 'personnalité' unique, résultant en une plus grande diversité de la colonie sans avoir à changer le réseau de neurones commun : elles ont toutes le même cerveau, mais pas les mêmes goûts.

Malheureusement, nous n'avons pas eu assez de temps pour trouver un ensemble d'hyper-paramètres fonctionnels. Comme cette méthode est plus complexe, elle est également plus sensible à la part aléatoire de l'apprentissage et nous avons rencontré des difficultés à produire des résultats intéressants. Depuis un point de vue théorique, il n'y a pas non plus de garantie que l'apprentissage par Q-value soit maintenu lorsque plusieurs récompenses contradictoires sont apprises par un même agent, mais d'un autre côté, nous ne voyons pas de raisons pour lesquelles cela ne fonctionnerait pas. Nous mettrons à jour cet article si nous parvenons à faire fonctionner ce système ! Pour le moment, tout fonctionne bien, mais l'entraînement donne des résultats équivalents à la version plus simple du modèle.

Conclusion, questions ouvertes et développements futurs

Notre objectif initial était peut-être ambitieux : nous imaginions déjà des colonies se battant les unes contre les autres pour la nourriture, des fourmis poussant des rochers pour dégager la voie ou pour créer des ponts au-dessus de rivières... Il faut toujours viser les étoiles !

Les résultats, même après seulement 150 épisodes, sont très prometteurs et nous voyons définitivement des comportements émergents dans les sociétés de fourmis, ce qui était notre principal intérêt. À présent, nous ressentons le besoin de poursuivre les expériences, mais c'est déjà la fin du temps qui nous était imparti pour ce projet. Cependant, cela ne nous empêchera pas de mettre à jour cet article !

Nous avions même déjà implémenté dès le début les rochers déplaçables par les fourmis. En fonction du poids des rochers et du nombre de fourmis poussant dans la même direction, ils bougeaient plus ou moins vite. Mais c'était encore un peu instable, et nous avons vu des fourmis se retrouver coincées à l'intérieur de murs, ainsi que d'autres choses peu désirables. Nous avons décidé de les retirer de nos démonstrations.

Dans des développements futurs, nous aimerions laisser la possibilité aux fourmis d'agir sur leurs mandibules de façon à choisir entre ramasser et porter de la nourriture et combattre des menaces comme d'autres fourmis hostiles. Nous aimerions également rendre les cartes plus complexes et offrir aux fourmis la possibilité de communiquer plus facilement via un vecteur d'état visible par d'autres fourmis voisines. Mais avant tout cela, nous ré-implementerions notre simulation en C++ en utilisant la programmation parallèle sur GPU : nous tenons un scoop, Python est lent.

Nous avons seulement pu voir le début de ce que nous attendions comme comportements émergents, mais nous pensons que si nous avions mis plus d'outils à disposition de nos agents, et des problèmes plus complexes à résoudre, nous aurions vu des solutions de plus en plus intelligentes apparaître !

Bien... De très nombreuses choses peuvent être faites, partant de là où nous nous sommes arrêtés ! Peut-être qu'un autre chapître suivra ? Qui sait. Soyez préparés.

Liens & Références

Pour obtenir le code Python complet du projet, visitez notre github :
https://github.com/WeazelDev/AntsRL

Références:

• “DQN”; Mnih et al. 2015
• A (Long) Peek into Reinforcement Learning (blogpost)
• Branching Q-learning, A. Tavakoli, 2019
• Reinforcement Learning, an Introduction - R. Sutton
• Deep Reinforcement Learning for Swarm Systems, M.Hüttenrauch 2019

Les principaux modules utilisés durant tout ce projet :

• Numpy - pour la simulation
• Pytorch - pour la définition de l'agent et l'entraînement du DQN
• PyGame - pour la visualisation